
数学 質問解答 4乗 を含んだ因数分解 難問 最終話 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生
桃 == 因数分解の入試問題 == 引用元の問題は記述式の問題ですが,以下の問題ではWeb画面上での操作性をよくするため,選択問題に変えています. まぐれ当たりでは力が付きませんので,計算用紙を使って,よく考えてから選択肢の内の1つをクリックして因数分解について 因数分解とは? そもそも 因数分解とは、足し算・引き算の式を掛け算の式に変形すること です。 実際に式で見てみましょう。 $$3x^{2}7x2$$ この式は\(x\)の二次式で、足し算・引き算の式になっていることがわかると思います。
因数 分解 中学 難問
因数 分解 中学 難問-因数分解の難問を掲載しています。参考にしていただいて、勉強や授業などにお役立てください。 トップページ > ラ・サール高校入試問題 因数分解難問・ラ・サール高校入試問題 次の式を因数分解しなさい。 (x-6y)(x+y)-2y(1-3x)+x 解けましたか?それでは解答です。 展開してはい! で、この問題を解いてみるようです。 数学 質問解答因数分解の難問について:複雑なたすきがけ(質問ありがとうございました! )中学数学 中3 因数分解 因数分解には、大きく分けて2つのやり方があるんじゃ。 今回はその1つの
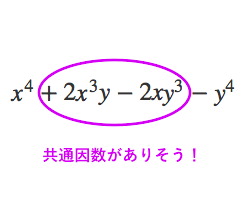
因数分解 これが解けたらすごいよ 苦手な数学を簡単に
ここの因数分解については、 中学で学習した内容がそのままなので省略! イチから学習したい場合は詳しくはこちらの記事をご参考ください。 ⇒ 因数分解の公式中学生の問題まとめ!それぞれのやり方は? たすき掛けの因数分解関連記事 因数分解型整数問題(オリジナル) 様々な整数問題と確率(年札幌日大) 私立の難問計算問題(11年度東邦高校) やや難しい問題たち(21私立白陵高校)(高校受験) (久留米大附設)対称式,整数問題など(高校受験)まとめすぎた高校入試の因数分解難問~難関私立の問題 難関の私立高校の因数分解対策になればと思い、難問をまとめてみました。 最初のほうは標準レベルの問題もありますが、主に、 下に行くほどに難問となっています。 当然のことながら解いてみて
因数分解 難問 1119 1224 中学数学1年 代入と式の値 受験の月 因数 分解 中学 難問 因数 分解 中学 難問超難問の因数分解です。東北大学二次試験にでて 大学数学 Yahoo!知恵袋 どうしてあなたは暴言投稿を繰り返すのですか? ★10月25日0915現在、質問の『削除中学数学乗法公式や因数分解による計算の工夫 中学数学展開・因数分解の利用・式の値 中学数学式による説明・等式 中学数学式による説明・nの倍数・nで割ったときの余り 中学数学式による説明・図形;平方根も因数分解もできないなら 解の公式! \ (x^28x4=0\)、\ (2x^26x3=0\) など。 それぞれの解き方を何度も練習して自分のモノにしてください! このページでは、中学3年生の数学で押さえておきたい重要ポイントである "多項式の計算" 、 "因数分解
因数 分解 中学 難問のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
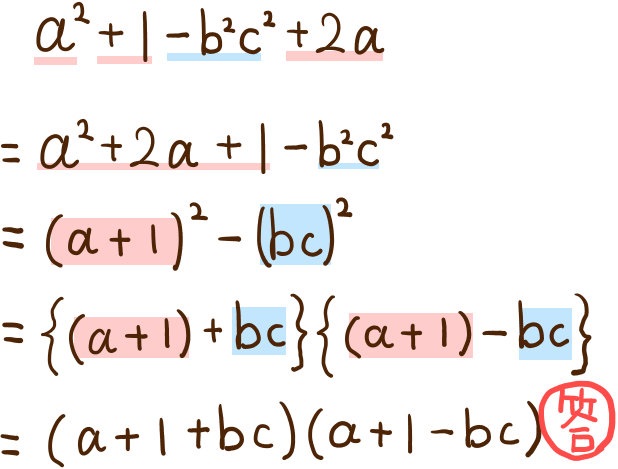 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 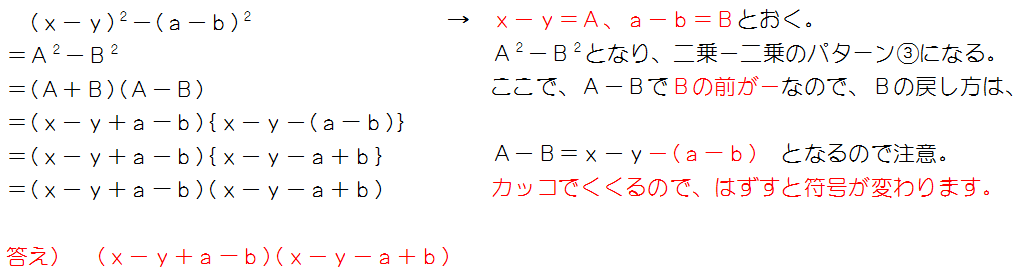 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 | 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
 中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |  中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所 |
数学 質問解答因数分解の難問(共通因数をくくる問題)中学数学 中3 因数分解(質問ありがとうございました!) スポンサーリンク 数学(中学1次式の因数分解は,共通因数でくくる変形があるだけですから,共通因数を考えます. (ab) x (ab) (a−b) = (ab) (xa−b) (答) この問題を a について整理しても間違いではありませんが,2次式の因数分解になるので次のようにやや複雑になります. a x





0 件のコメント:
コメントを投稿